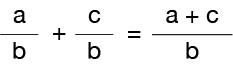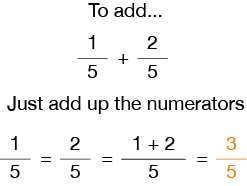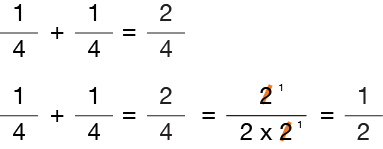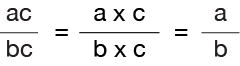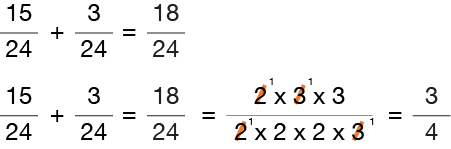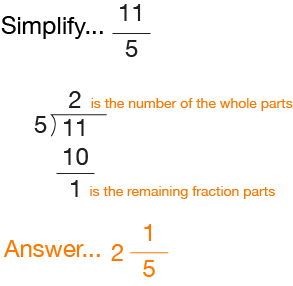Adding Fractions with the Same Denominators
Adding fractions with the same denominators is pretty straightforward when you follow the rules. This lesson covers adding fractions with same denominator. We will include all of the information you will need to make working with common denominator problems a breeze!
The equation above shows the Rule for addition. So, if your are dealing with the same (common) denominator (b), the answer is the sum of the numerators (a and c) over their common denominator. Remember that a fraction refers to the number of parts in a “whole”, and the WHOLE that we are talking about is always the number in the denominator (on the bottom). So, all we have to do is add up the parts and keep our same point of reference.
Instructions for adding fractions with the same denominator
To add fractions, the denominators must be equal. Complete the following steps to add two fractions.
- Build each fraction (if needed) so that both denominators are equal.
- Add the numerators of the fractions.
- The new denominator will be the denominator of the built-up fractions.
- Reduce or simplify your answer, if needed.
- Factor the numerator.
- Factor the denominator.
- Cancel-out fraction mixes that have a value of 1.
- Re-write your answer as a simplified or reduced fraction.
REMEMBER: We DO NOT add denominators
That’s all there is to it!
Here’s an example of adding fractions with the same denominator…
Do you want to take a moment to check your work? Try our new Adding Fractions Calculator for adding up to 5 fractions, whole numbers, mixed numbers or improper fractions with the same or different denominators.
Now that you have this part of adding fractions down, let’s dig a little deeper…
You do want to be a “whiz” at fractions? Right?
Okay then!
It would be great if the rule as stated above was all you needed to know about adding fractions. But there are still a few more things we need to talk about to complete this lesson. So, let’s get right to it.
Click here to learn how to re-write your answer as a simplified or reduced fraction.
How to Simplify Your Answers
Sometimes when you add fractions of any type, you will need to simplify your answer. What that really means is that you must show your results in the “best” fractional form possible. As a result, here are a few more things to think about…
First, your answer may be a higher equivalent fraction, which is better represented in its reduced form. Many teachers will insist that you reduce a fraction whenever possible.
Also, adding two fractions could result in what’s called an improper fraction. This is where the numerator is larger than the denominator. To write these answers in their simplest form you will have to convert them to a mixed number. This will show a representation of the Whole Parts and the Fractional Parts.
So let’s continue with some detailed information about adding fractions in these special cases.
Reducing Fractions To Their Lowest Equivalent
Here’s the situation. You have added the fractions okay, but your answer may not be showing the lowest equivalent fraction. So how do you make sure when you are adding fractions that your answer is shown in its lowest equivalent?
Let’s use an easy example of adding fractions so you will get the idea…
Notice that the original answer to adding the fractions our sample problem is “2/4.” To determine if our answer is in its simplest form, we must factor the numerator and the denominator into its prime numbers.
Click here for a review of prime numbers.
The factors of a number are numbers that when multiplied together will equal that number. The easiest way to be sure that you have accounted for ALL of the factors of a number contained in a fraction is to break them down into prime numbers.
What we are looking for are the prime numbers that are common factors in both the numerator and the denominator of a fraction. If we find these common factors, we can then cancel them out. The results will be the lowest fractional equivalent fraction.
Since “2” is a common factor in both the numerator and denominator of our example, it indicates that our answer is not a fraction in its simplest form. Therefore, we will cancel out (/) one of the 2’s in both the numerator and denominator by dividing by “2”. The results is a reduced fraction in its simplest form.
Here’s the Rule…
Always keep in mind…
Whatever you do to the numerator of a fraction you must also do to the fraction’s denominator. So if you have to divide the numerator by a number, you must also divide the denominator by the same number. That way you will not change the overall value of the fraction.
Let’s add a little tougher fraction to be sure you’ve got it…
In this problem, a “2” and a “3” can be found as factors in both the numerator and the denominator of a fraction. Notice how we only cancel-out one-for-one! First we divide the numerator and denominator by “2”, then divide both the numerator and denominator by “3.” So what is left in the numerator is 1 x 1 x 3 = 3 and the denominator is 1 x 2 x 2 x 1 = 4. That leaves use with a reduced fraction equal to 3/4.
Simplify Improper Fractions
You may remember that an improper fractions is where the numerator has a greater value than that of the denominator. So each time you add two fractions and your answer ends up as an improper fraction, you must simplify your answer. The results will be in the form of a mixed number.
To convert an improper fraction into a mixed number, just divide the numerator by the denominator. The results will be a whole number part and a fractional part.
Here is an example…
As you can see, this is a pretty straightforward operation. But keep in mind that if there is no remainder, the answer is the WHOLE NUMBER only.
Now you have an uncomplicated way to add fractions with the same denominators.
[fusion_separator style_type=”shadow” top_margin=”40″ bottom_margin=”40″ sep_color=”” icon=”” width=”” class=”” id=””/]