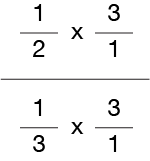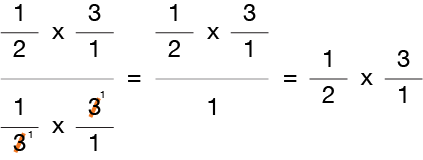Dividing Fractions Has A Weird Rule
Dividing fractions can be a little tricky. It’s the only operation that requires using the reciprocal. Using the reciprocal simply means you flip the fraction over, or invert it.
For example, the reciprocal of 2/3 is 3/2.
After we give you the division rule, we will show you WHY you have to use the reciprocal in the first place.
But for now…
Here’s the Rule for Division
To divide, convert the fraction division process to a multiplication process by using the following steps.
- Change the “÷” (division sign) to “x” (multiplication sign) and invert the number to the right of the sign.
- Multiply the numerators.
- Multiply the denominators.
- Re-write your answer in its simplified or reduced form, if needed
Once you complete Step #1 for dividing fractions, the problem actually changes from division to multiplication.
Example 1: Dividing Fractions by Fractions
1/2 ÷ 1/3 = 1/2 x 3/1
1/2 x 3/1 = 3/2
Simplified Answer is 1 1/2
Example 2: Dividing Fractions by Whole Numbers
1/2 ÷ 5 = 1/2 ÷ 5/1
(Remember to convert
whole numbers to fractions, FIRST!)
1/2 ÷ 5/1 = 1/2 x 1/5
1/2 x 1/5 = 1/10
Example 3: Dividing Whole Numbers by Fractions
6 ÷ 1/3 = 6/1 ÷ 1/3
(Remember to convert
whole numbers to fractions, FIRST!)
6/1 ÷ 1/3 = 6/1 x 3/1
6/1 x 3/1 = 18/1 = 18
Now that’s all there is to it. The main things you have to remember when you divide is to convert whole numbers to fractions first, then invert the fraction to the right of the division sign, and change the sign to multiplication.
The “divisor” has some other considerations you should keep in mind…
Special Notes!
- Remember to only invert the divisor.
- The divisor’s numerator or denominator can not be “zero”.
- Convert the operation to multiplication BEFORE performing any cancellations.
I promised to try to explain why the rule requires inverting the divisor.
Here goes..
Why Dividing Fractions Requires Inverting The Divisor
Let’s use our simple example to actually validate this strange Rule for division.
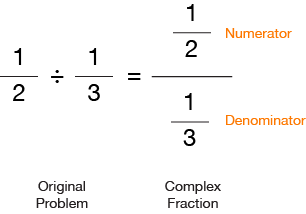
If you really think about it, we are dividing a fraction by a fraction, which forms what is called a “complex fraction”. It actually looks like this…
When working with complex fractions, what we want to do first is get rid of the denominator (1/3), so we can work this problem easier.
You may recall that any number multiplied by its reciprocal is equal to 1. And since, 1/3 x 3/1 = 1, we can use the reciprocal property of 1/3, (3/1), to make the value of the denominator equal to 1.
You might also recall that whatever we do to the fraction’s denominator, we must also do to its numerator, so as not to change the overall fraction “value”.
So let’s multiply both the numerator and denominator by 3/1…
Which gives us…
Here’s what happened…
By multiplying the numerator and denominator of our complex fraction by 3/1, we were then able to use the reciprocal property of a fraction to eliminate the denominator. Actually, without our helpful Rule, we would have to use all of the steps above.
So, the Rule for dividing fractions really saves us a lot of steps!
Now that’s the simplest explanation I could come up with for WHY and HOW we end up with a Rule that says whenever we divide fractions, we must invert the divisor!