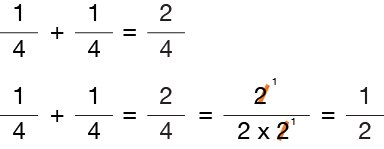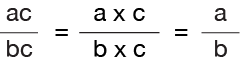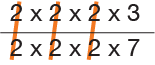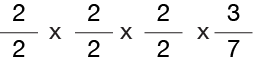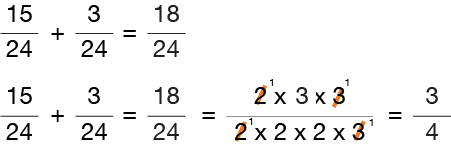Reducing Fractions Through Factorization
Reducing fractions is another way of saying, “finding the lowest equivalent fraction.” That’s because you are normally trying to reduce a proper fraction to its simplest term.
Note: The term “reduce” usually refers to proper fractions (the numerator is smaller than the denominator). Whereas, the term “simplify” generally refers to improper fractions (the numerator is larger than the denominator).
When reducing a proper fraction, follow these steps:
- Factor the numerator.
- Factor the denominator.
- Cancel-out fraction mixes that have a value of 1.
- Re-write your answer as the reduced fraction.
Let’s use an easy example of reducing fractions so you will get the idea…
Notice that the original answer to adding the fractions our sample problem is “2/4.” To determine if our answer is in its simplest form, we must factor the numerator and the denominator into its prime numbers.
Click here for a review of prime numbers.
The factors of a number are numbers that when multiplied together will equal that number. The easiest way to be sure that you have accounted for ALL of the factors of a number contained in a fraction is to break them down into prime factors.
What we are looking for are the prime numbers that are common factors in both the numerator and the denominator of a fraction. If we find these common factors, we can then cancel them out. The results will be the lowest fractional equivalent fraction.
Since “2” is a common factor in both the numerator and denominator of our example, it indicates that our answer is not a fraction in its simplest form. Therefore, we will cancel out (/) one of the 2’s in both the numerator and denominator by dividing by “2”. The results is a reduced fraction in its simplest form.
Here’s the Rule…
Here’s Another Example:
To reduce 24/56 we factor the Numerator (24 = 2 x 2 x 2 x 3) and then factor the Denominator (56 = 2 x 2 x 2 x 7).
In this example all of the 2s are eliminated because there are an equal number of 2s in both the numerator and denominator. They cancel-out one-for-one. That’s what we mean by a fraction mix that has the value of “1”.
The correct answer for the example above is a reduced fraction that’s equal to 3/7.
Here’s another way to look at reducing 24/56.
You already know that 2/2 = 1, so…
is the same as
which is equal to 1 x 1 x 1 x 3/7
Therefore, you would re-write your answer as 24/56 is equal (or equivalent) to 3/7.
That’s the basics of reducing proper fractions, regardless of size.
Always keep in mind…
Whatever you do to the numerator of a fraction you must also do to the fraction’s denominator. So if you have to divide the numerator by a number, you must also divide the denominator by the same number. That way you will not change the overall value of the fraction.
Let’s add a little tougher fraction to be sure you’ve got it…
In this problem, a “2” and a “3” can be found as factors in both the numerator and the denominator of a fraction. Notice how we only cancel-out one-for-one! First we divide the numerator and denominator by “2”, then divide both the numerator and denominator by “3.” So, what’s left in the numerator is 1 x 1 x 3 = 3 and the denominator is 1 x 2 x 2 x 1 = 4. That leaves use with a reduced fraction equal to 3/4.
A sure-fire check that you fraction is in lowest terms is when the Greatest Common Factor (GCF) of its numerator and denominator is 1.