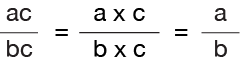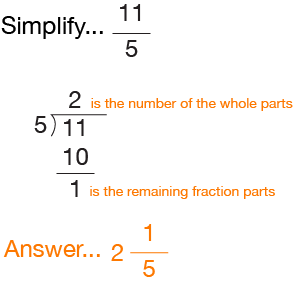Simplifying fractions is often required when your answer is not in the form required by the assignment. As a matter of fact, most math instructors will demand that you always put the resulting fraction in its simplest form.
Generally speaking, there are two occasions where simplifying your answer may be necessary.
- Actually, your answer may be a higher level equivalent proper fraction, which is better represented in its reduced form or lowest term. Many teachers will insist that you reduce your answer, whenever possible.
- Also, many operations will often result in what’s called an improper fraction. This is where the numerator is larger than the denominator. To write these answers in their simplest form you will have to convert them to a mixed number. This will show a representation of the Whole Parts and the Fractional Parts.
For the purposes of this discussion, let’s say both situations are called simplifying your answer.
Reducing Fractions To Their Lowest Equivalent
Here’s the Rule for simplifying or reducing fractions to their lowest term…
Whatever you do to the numerator of a fraction you must also do to the denominator. So if you have to divide the numerator by a number, you must also divide the denominator by the same number. That way you will not change the overall value of the fraction.
In our rule, we have divided the numerator and the denominator by “c” to arrive at our simplified answer.
Here’s the situation. You have added the fractions okay, but your answer may not be showing the lowest equivalent fraction. The easiest way to know for sure that your answer is in its simplified form is to breakdown both the numerator and the denominator into prime numbers.
This process is called Prime Factorization.
Here’s an example so you’ll get the idea…
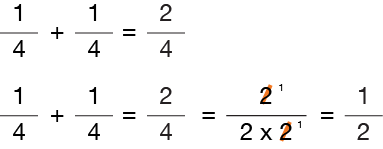
Notice that the original answer after adding the fractions is “2/4.” To determine if our answer is in its simplified form, we must factor the numerator and the denominator into its prime numbers.
What we are looking for are the prime numbers that are common to both the numerator and the denominator. If we find these common numbers, we can then cancel them out. The results will be a fraction simplified to its lowest equivalent fraction.
Since “2” is a common factor in both the numerator and denominator of our example above, it indicates that our answer is not in its simplest form. Therefore, we cancelled out (/)one of the 2’s in both the numerator and denominator by dividing by “2”, one for one. The results is a “simplified fraction” reduced to its lowest term.
Got it?
GREAT!
Now let’s look at…
Simplifying Improper Fractions
You may remember that an improper fractions is where the numerator has a greater value than that of the denominator. So each time you perform an operation on fractions and your answer ends up as an improper fraction, you will usually need to simplify your answer. The results will be in the form of a mixed number.
So to convert an improper fraction into a mixed number, we just divide the numerator by the denominator. The results will be a whole number part and a fractional part.
Here is an example…
As you can see, this is a pretty straightforward operation. But keep in mind that if there is no remainder, the answer is the WHOLE NUMBER only.
Be sure to look closely at the resulting fraction to ensure it’s in simplest terms. If not, you will need to reduce it.
So as you can see, simplifying fractions is no-big-deal. Just follow the steps above, and putting fraction in their simplified form will be like a “walk in the park.”