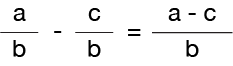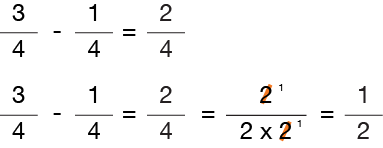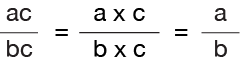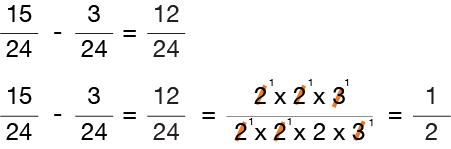Subtracting Fractions With The Same Denominators Is “A Piece Of Cake!
Subtracting fractions with like denominators is just as easy as adding them.But we will take nothing for granted. So you can expect the same detailed explanation as always. So let’s start our discussion as if this were the first page you saw upon arrival to our site.
So,…
The Rules for subtracting fractions state that denominators must be the same. Period. And since our denominator are already the same…
Let’s begin with the Rule….
The equation above shows the Rule for subtracting fractions with the same denominator. So, if you are subtracting fractions with the same (common) denominator (b), the answer is the difference between the numerators (a – c) over their common denominator.
Remember that a fraction refers to the number of parts in a “whole“, and the WHOLE that we are talking about is always the number in the denominator (on the bottom). So, when subtracting fractions that refer to the “same” whole, all we have to do is subtract the parts and keep our same point of reference.
Yep!
In the next section, I give a couple of examples along with how to reduce fractions when needed, using prime factorization.
Reducing Fractions After You Subtract
Here’s the situation. You have subtracted the fractions, but your answer still may not be showing the lowest equivalent fraction. So how do you make sure your answer is shown in its lowest equivalent?
Let’s use an easy example so you will get the idea…
Notice that the original answer to our sample problem is “2/4.” To determine if our answer is in its simplest form, we must factor the numerator and the denominator into its prime numbers. Click here for a review of prime numbers.
What we are looking for are the prime numbers that are common to both the numerator and the denominator. If we find these common numbers, we can then cancel them out. The results will be the lowest equivalent fraction.
Since “2” is a common factor in both the numerator and denominator of our example, it indicates that our answer is not in its simplest form. Therefore, we will cancel out (/) one of the 2’s in both the numerator and denominator by dividing by “2”. The results is a reduced fraction in its simplest form.
Here’s the Rule…
Always keep in mind…
Whatever you do to the numerator of a fraction you must also do to the denominator. So if you have to divide the numerator by a number, you must also divide the denominator by the same number. That way you will not change the overall value of the fraction.
Let’s do a little tougher problem to be sure you’ve got it…
In this problem, a “2” and a “3” can be found in both the numerator and the denominator. Notice how we only cancel-out one-for-one! First we divide the numerator and denominator by “2”, then divide both the numerator and denominator by “3.” So what is left in the numerator is 1 x 1 x 1 = 1 and the denominator is 1 x 1 x 2 x 1 = 2. That leaves use with a reduced fraction equal to 1/2.
See what we just did?
GREAT!
Now there you have it, all you need to be a “master” at subtracting fractions with the same denominator… and a whole lot more.